Calculation of Mitral Valve Area by Continuity Equation Using Velocity-Time Integral From Mitral Valve Orifices After Mitral Clip
Abstract
Background. This study investigates the hemodynamics of a dual-orifice mitral valve after mitral valve clip closure (MVCC) in patients with functional and nonfunctional mitral regurgitation (MR). If inflow velocity-time integral (VTi) of both orifices is equal, then the standard continuity equation can be applied to calculate the total mitral valve area (MVA). Methods and Results. Adults undergoing MVCC placement were prospectively enrolled. With transesophageal echocardiography (TEE), the vena contracta (VC) of the medial and lateral mitral valve (MV) orifices were determined using color-flow Doppler and dual MV orifice areas were calculated. Valve orifices were classified as large vs small based on VC diameters. Continuous-wave Doppler measurements from both orifices were obtained. Forty-nine patients with severe MR (functional, n = 18) were enrolled. The VTi, mean gradient, peak gradient, and mean velocity of the larger vs smaller orifice were not significantly different, irrespective of MR etiology (P=nonsignificant). There was no difference in these parameters between large and small orifice regardless of MR mechanism (P=nonsignificant). There were no differences in the means of MVA as derived from either large or small VTi-derived and VC-derived areas (P=nonsignificant). Conclusions. Mitral valve inflow hemodynamics were the same regardless of the size differences between the large and small orifices. Therefore, total MVA can be calculated using the continuity equation in patients irrespective of MR mechanism. This allows for a derivation of total MVA at the time of MVCC placement to evaluate for mitral stenosis.
J INVASIVE CARDIOL 2022;34(8):E581-E587. Epub 2022 June 24.
Key words: mitral regurgitation, mitral valve clip closure, transesophageal echocardiography
Among individuals with moderate or severe valvular heart disease, mitral regurgitation (MR) is the most common valvular pathology and it is associated with significant morbidity.1,2 Secondary MR develops from lateral displacement of papillary muscles, leading to valve malcoaptation due to left ventricular enlargement. Mitral valve clip closure (MVCC) for severe MR has emerged as an effective percutaneous treatment strategy in select patients with functional and nonfunctional MR.3,4 Moreover, the COAPT trial demonstrated a mortality benefit in patients with heart failure with reduced ejection fraction and severe secondary MR.4,5 Although MVCC can be effective in the reduction of MR, it also has the potential to create hemodynamically significant iatrogenic mitral stenosis.6 Recognition of significant mitral stenosis during the MVCC placement procedure has largely been dependent upon transesophageal echocardiography (TEE) measurements. These measurements include estimation of peak gradient, mean gradient, and mitral valve area (MVA) via pressure half-time and 3-dimensional (3D)-directed planimetry.7 However, transmitral valve gradients are flow-rate dependent and as such, may not always reflect the severity of mitral stenosis. Mitral valve area derived by pressure half-time after MVCC has not been fully validated, as prior studies have shown that changes in MV orifice area may not be well estimated by pressure half-time after intervention.8,9 The cross-sectional planes for optimal planimetry of each orifice often differ. Therefore, the determination of anatomical orifice area by planimetry is not always feasible under the time constraints of the MVCC procedure. Derivation of MVA after MVCC is complex because a dual-inlet orifice is created, and this potentially invalidates the standard continuity equation, which requires that flow across the MV must be the same as the flow in the left ventricular outflow tract (LVOT). Echocardiographic methods rely upon the velocity-time integral (VTi) to derive flow or stroke volume. With 2 mitral inlet orifices after MVCC, each orifice has a VTi that may not necessarily be equal. Consequently, calculations of MVA by the standard continuity equation would be invalid. However, if the VTi in both of the created orifices is the same, the standard continuity equation would theoretically still apply. Mitral valve dual-inflow anatomy following MVCC is complex and varies between functional vs nonfunctional etiologies of MR. For this reason, the geometric alterations of the mitral inlet may be a factor in potential discrepancies between the hemodynamics of each orifice.
The current study was designed to assess the hemodynamics of the 2 mitral inflow orifices following MVCC in patients with and without functional MR. We hypothesized that the hemodynamics through either orifice would result in the same data, including VTi, mean velocity, peak gradient, and mean gradient, irrespective of MR mechanism. If true, these data would support the use of the continuity equation for the derivation of total MVA irrespective of orifice size following MVCC.
Methods
Study design and population. Adult patients with severe MR scheduled for MVCC placement were prospectively enrolled into functional or nonfunctional groups. Functional MR was defined as regurgitation secondary to primary cardiomyopathy (ie, dilation of the left ventricle). Only patients with severe MR prior to MVCC placement were included. Mitral regurgitation was graded as severe if color jet area was in excess of 10 cm2, or if the jet entrained along the left atrial wall and reached the posterior left atrium.10 Patients were studied after placement of the first MV clip if multiple clips were deployed using the MitraClip delivery system (Abbott Vascular). The study was approved by our institutional review board. Informed consent was obtained from each patient.
Image acquisition and storage. Transesophageal echocardiography was performed using an Epiq 7c (Philips Medical Systems) or GE Vivid 9 echocardiography machine (General Electric) interfaced with a multiplane TEE probe. After guidance of mitral clip placement, continuous-wave Doppler was aligned in parallel to color-flow Doppler inflow at the medial and lateral orifices of the MV. The vena contracta (VC) measurements of the medial and lateral orifices were determined using color-flow Doppler and typically obtained from a 60° transesophageal plane. Mitral valve lateral and medial orifice areas were calculated by the square of the vena contracta (VC) radii times pi. In each patient, the valve orifice with the largest VC was classified as large and the other orifice was classified as the small orifice. Continuous-wave Doppler inflow measurements from both orifices included mean velocity, mean and peak gradients, and VTi. The continuity equation was used to calculate the summed MVA (ie, the large orifice area plus the small orifice area) derived independently from the VTi of the large orifice, as well as independently with the VTi of the small orifice. Left ventricular ejection fraction was calculated by the biplane Simpson method using 4- and 2-chamber views.
Statistical analysis. All continuous values represent mean ± 1 standard deviation or ratios. Categorical values were analyzed with a Chi-squared test or Fischer’s Exact test, when appropriate. Mean values were compared using a paired Student’s t test or Wilcoxon signed-rank test, when appropriate. Unpaired values were compared using a Mann-Whitney U test. A least-squares linear-regression analysis was used to assess for correlations. A Bland-Altman analysis was performed to assess for bias. A probability (P)-valve <.05 was considered statistically significant. All statistical analyses were done using IBM SPSS, version 26.0 (IBM Corp). The data underlying this article will be shared upon reasonable request to the corresponding author.
Results
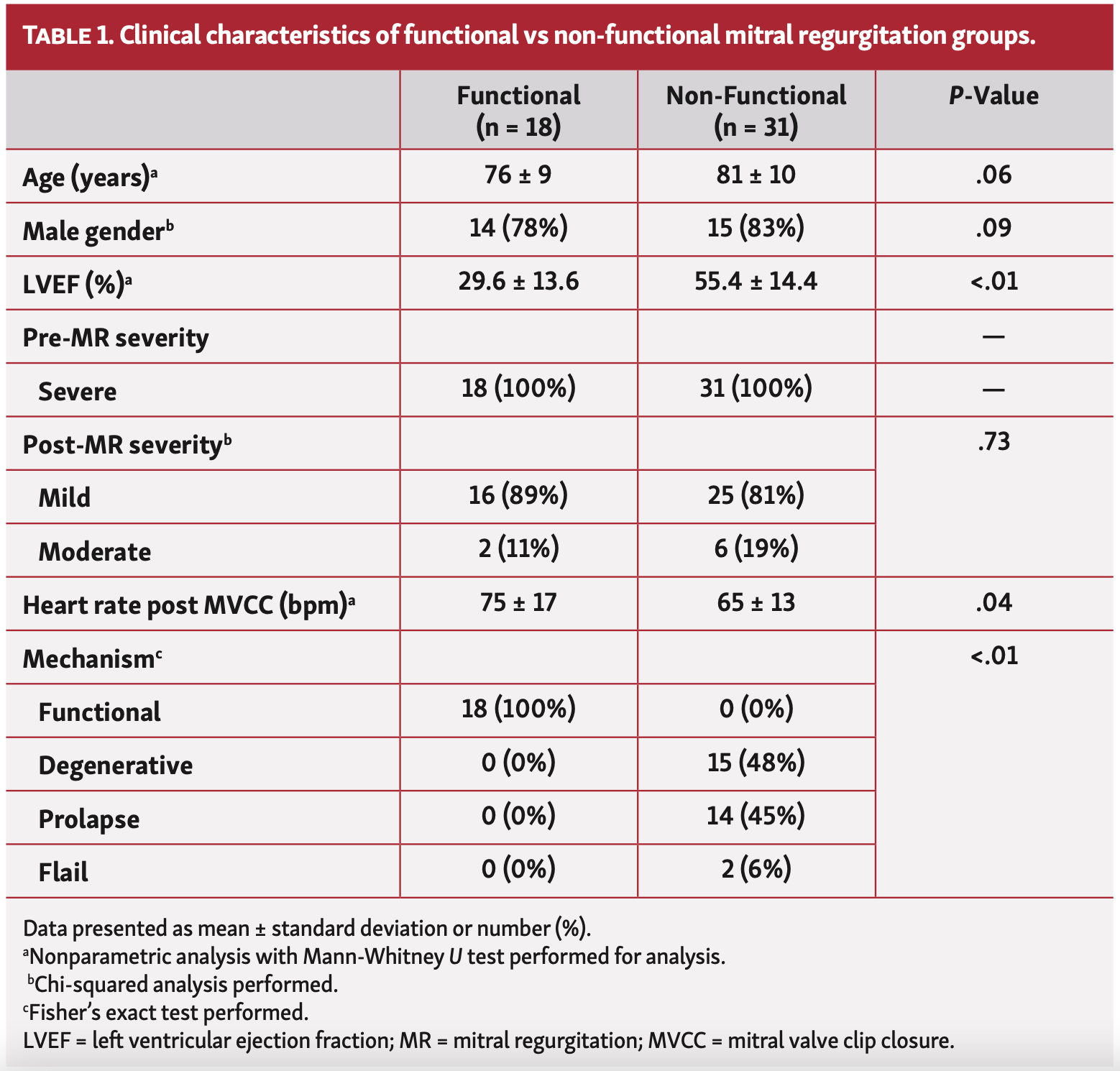
Study population. Forty-nine adult patients (29 males and 20 females) with severe MR who were scheduled for MVCC were enrolled. The average age was 78.0 ± 10.3 years (range, 43-97). Mechanism of MR was functional (n = 18) and nonfunctional (n = 31). The mechanisms of nonfunctional MR were thickened and degenerative leaflets (n = 15), prolapse (n = 14), and leaflet fail (n = 2). Mean ejection fraction was lower in the functional group vs the nonfunctional group. A complete characteristic profile is demonstrated in Table 1.
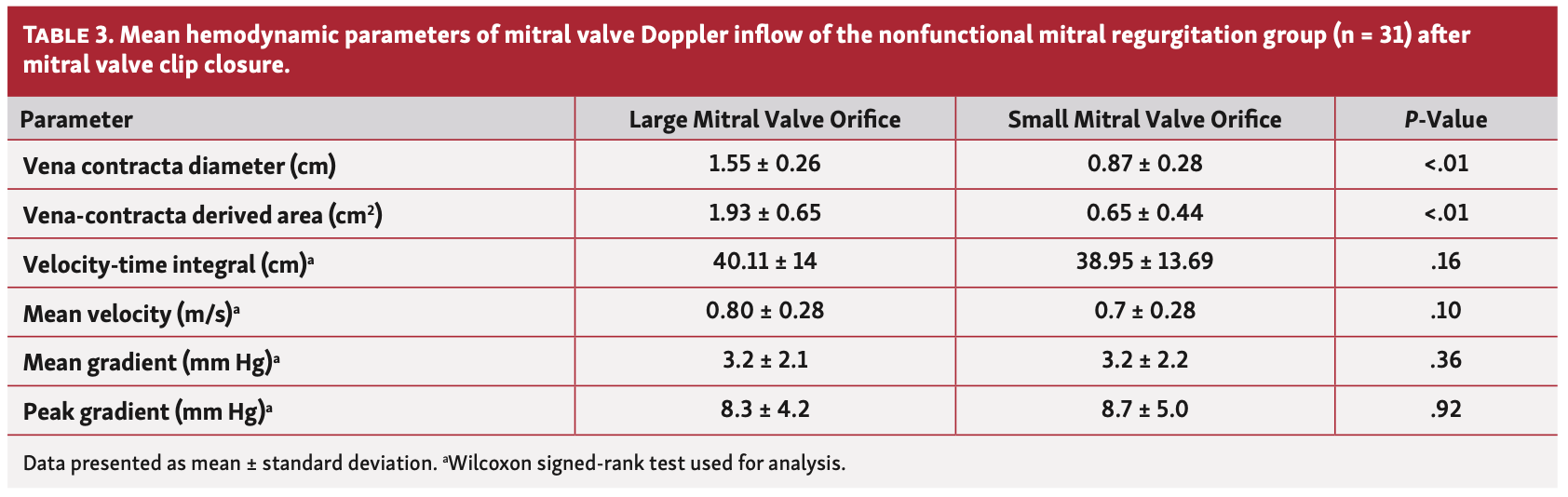
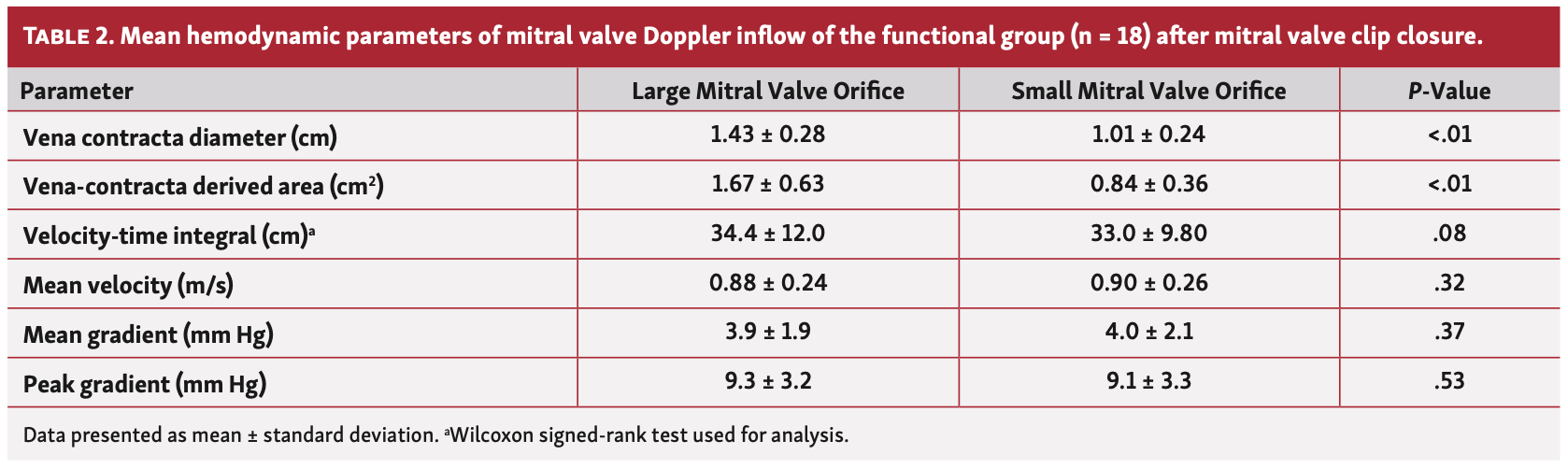
Mitral valve inflow hemodynamic. The average VC diameter of the large vs small orifice was significantly greater in the functional as well as the nonfunctional groups (P<.01 for both). Mitral valve areas of the large and small orifices were calculated using VC diameters and the averaged values were significantly different in the functional group (Table 2) vs the nonfunctional group (Table 3). The mean VTi of the large vs small orifice was not significantly different in either group (P=nonsignificant [NS] for both). Hemodynamic variables (ie, peak and mean gradients and mean velocity) of the large orifice vs small orifice did not differ in either group (P=NS for both). When comparing the functional and nonfunctional groups, the magnitudes of the average percent differences and absolute differences between the large orifice vs small orifice inflow Doppler variables (VTi, mean and peak gradients, and mean velocity) did not differ (Table 4). In the 41 patients with only mild MR after MVCC, there was no significant difference in VTi between the large orifice vs small orifice (37.8 ± 13.1 cm vs 36.4 ± 12.7 cm, respectively; P=NS).
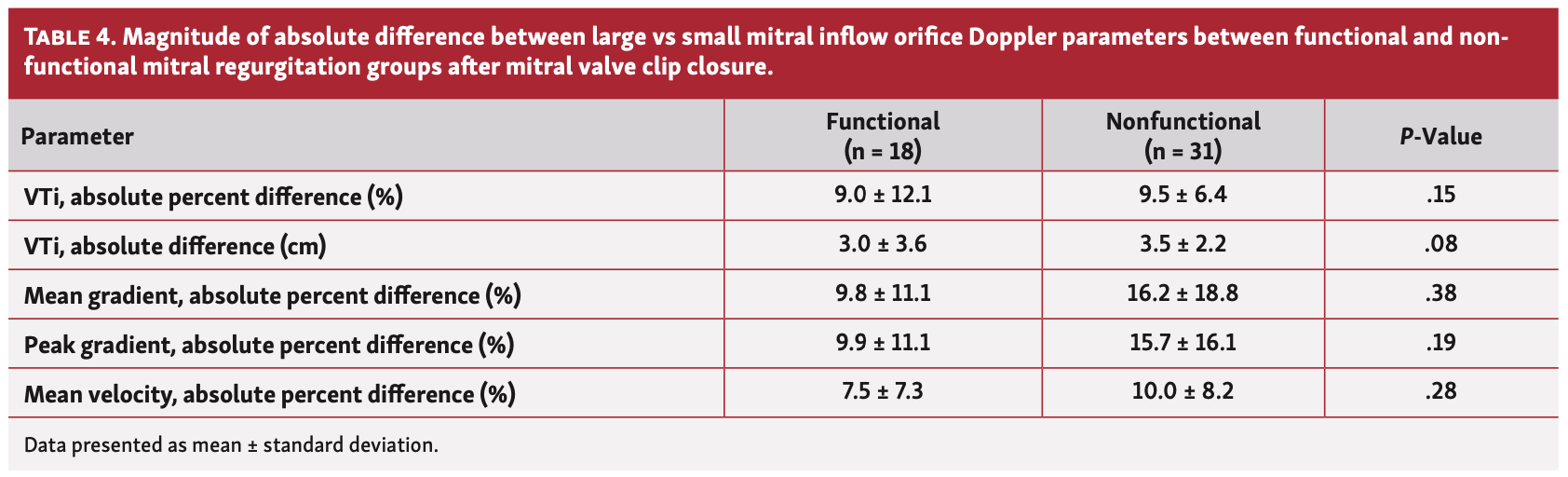
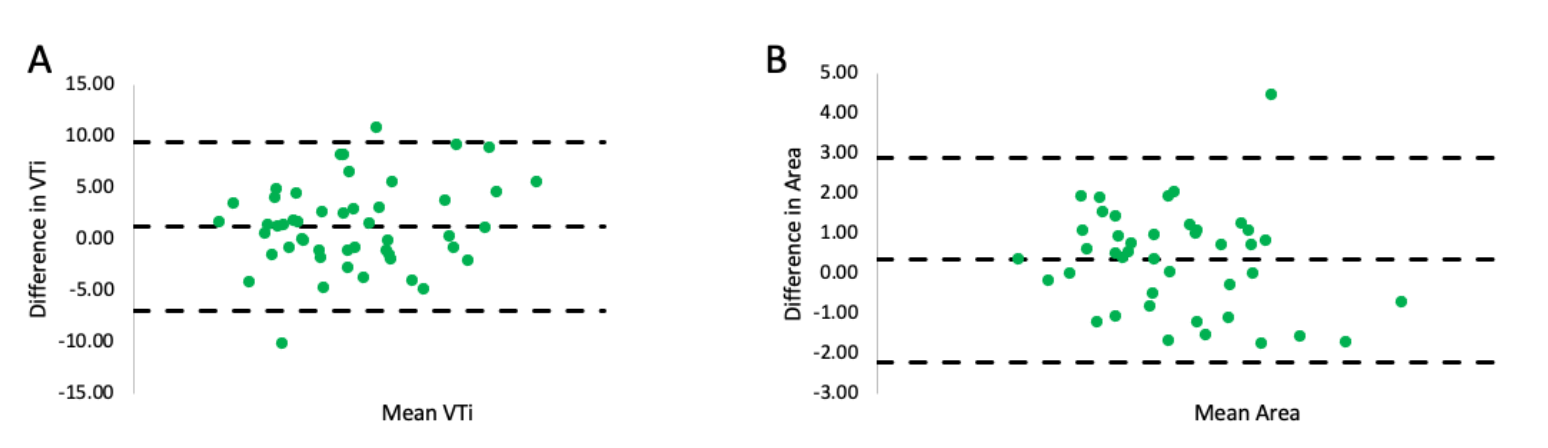
Mitral valve area calculations. The relative size of the large orifice vs small orifice was expressed as a ratio of the VC-derived large area vs small area. The relative difference between the VTi of the large orifice vs small orifice was expressed as a ratio of the VTi of the large orifice vs small orifice. The mean ratio of the VC-derived large orifice to small orifice area for all subjects (n = 49) was 3.6 ± 2.3 (range, 1.04-14.64). However, the mean VTi ratio was 1.03 ± 0.12 despite the marked differences in orifice area ratios (Figure 1). There was no difference in the means of VC-derived summed (ie, large + small orifice) areas and continuity-summed areas derived from either orifice (P=NS for both) (Table 5). A Bland-Altman plot demonstrated no bias in the measurements of summed MVA derived from VTi measurements of the large orifice vs small orifice (Figure 2A). There was no bias in the measurements of summed MVA as derived from the continuity equation vs VC (Figure 2B).

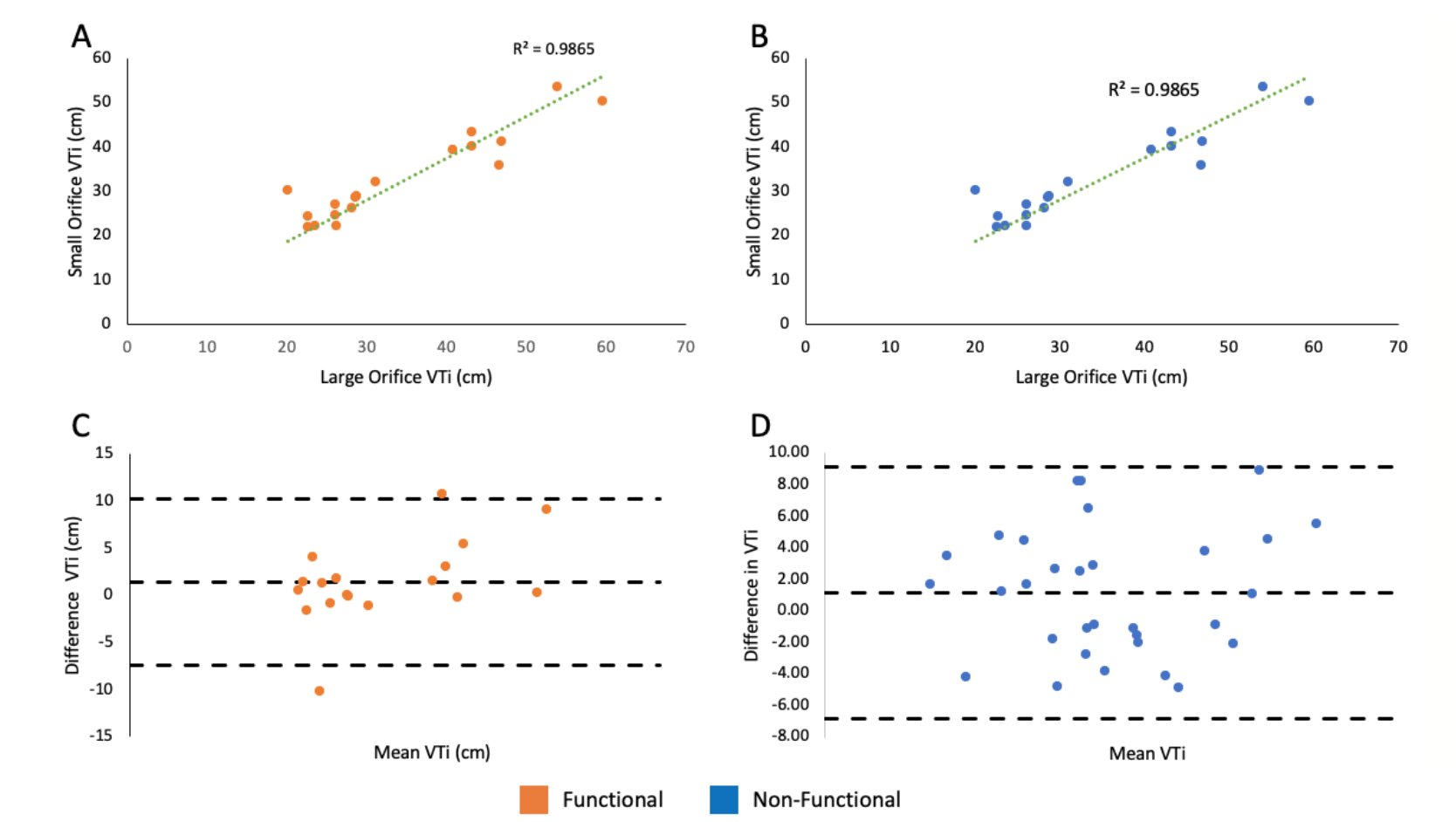
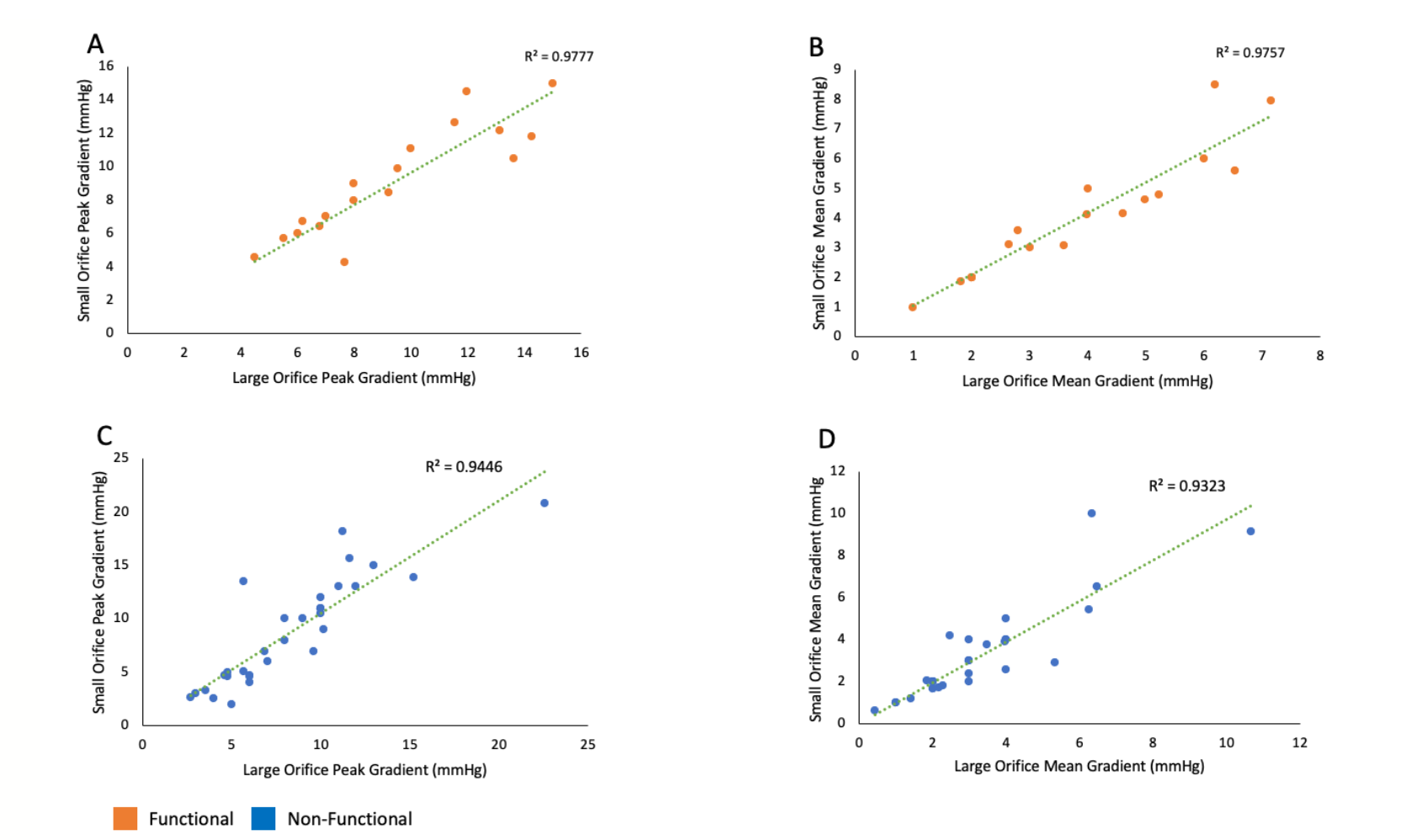
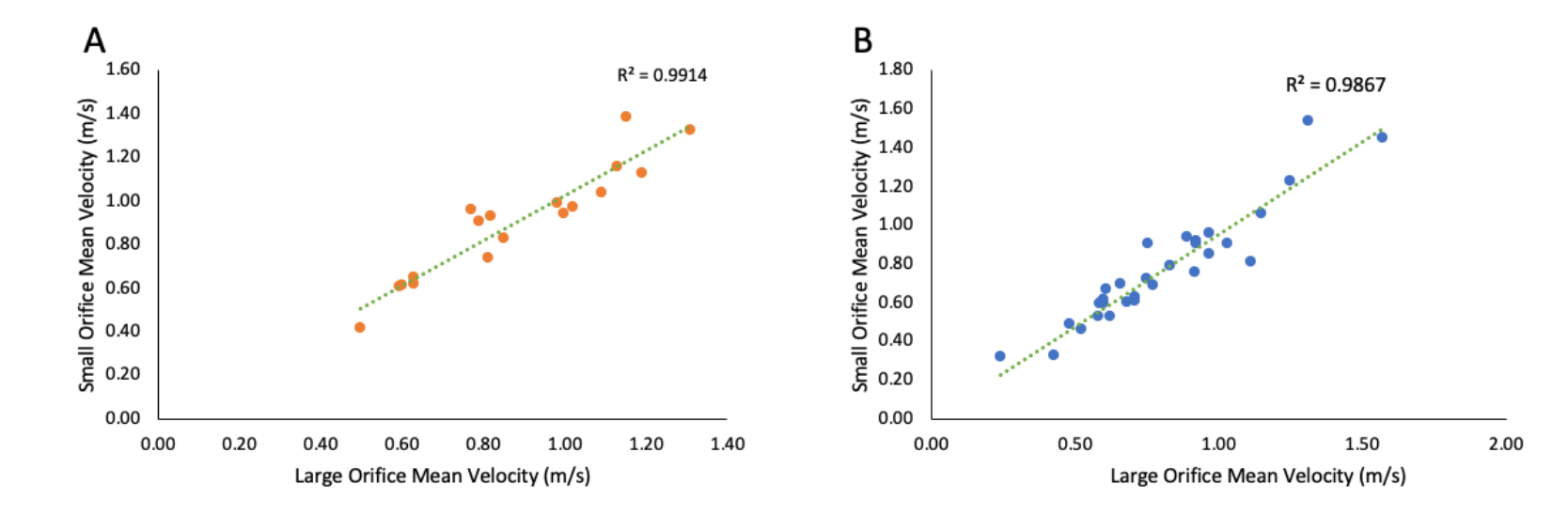
Correlations. There was a strong linear correlation between the VTi of the large orifice and small orifice in both functional and nonfunctional MR groups (P<.01) (Figure 3A and Figure 3B). A Bland-Altman plot showed no bias in the VTi measured using the large orifice vs small orifice (Figure 3C and Figure 3D). There were also significant linear correlations between the peak gradient, mean gradient, and mean velocity of the large orifice vs small orifice (Figure 4 and Figure 5).

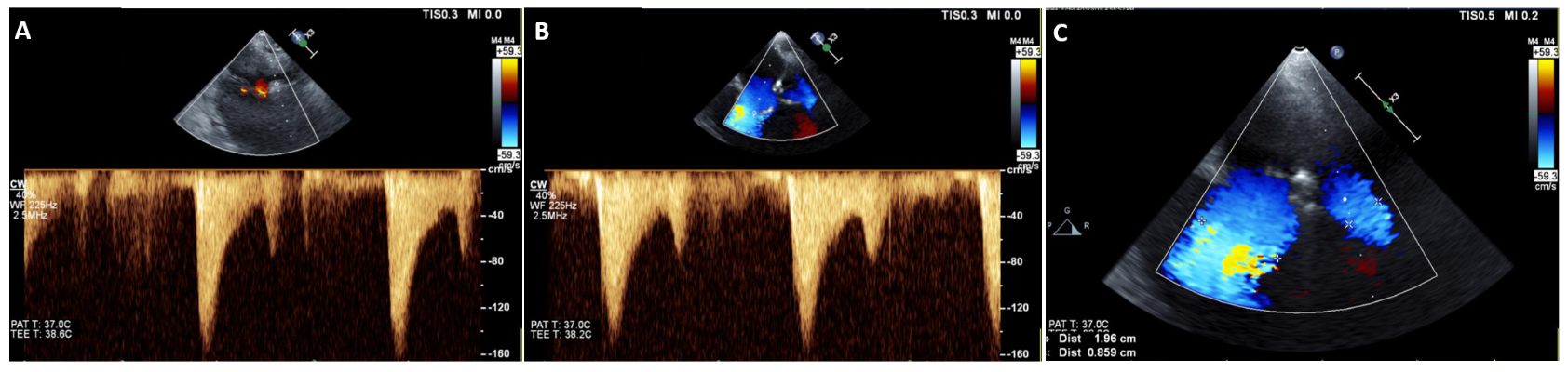
Case example. A case example is shown of a patient after MVCC with markedly different MV lateral and medial orifice VC diameters, but with virtually identical transmitral valve filling VTi measurements, velocities, and gradients (Figure 6).
Discussion
In the current study, we demonstrate that the hemodynamics (ie, peak and mean gradients and mean velocities) of the 2 mitral inflow orifices following MVCC are equal irrespective of functional and nonfunctional MR mechanisms. Furthermore, VTi of each orifice was equivalent irrespective of MR mechanism. Importantly, given that VTi measurements of the large orifice and small orifice are equal, then a total or summed MVA (ie, large MVA + small MVA) can be calculated with the continuity equation.
Mitral valve clip closure produces dual mitral orifices. Both orifices have the same left atrial driving pressure and the same downstream left ventricular receiving pressures during diastolic filling. Therefore, it is logical that the peak and mean pressure gradients across both orifices would be the same. In addition, since pressure gradients dictate transvalvular velocities, it would be expected that both orifices would have the same peak and mean velocities during diastolic filling. Furthermore, given that transmitral valve velocities are the same, the VTi measurements of the 2 orifices are expected to be the same. However, the flow across the larger orifice would be greater than that of the smaller orifice given that its cross-sectional area is larger. The flow across the large or small orifice equals its cross-sectional area x VTi. Therefore, VTi can be the same with differences in flow as dictated by cross-sectional area. A mathematical proof is dissected in Figure 7. The continuity equation should be an additional tool in the arsenal of the structural echocardiographer to identify mitral stenosis during MVCC deployment.
There have been several studies in the past decade evaluating the various cardiovascular hemodynamic effects of MVCC. This procedure can immediately reduce left atrial pressure, as well as improve cardiac output and left ventricular loading conditions.11,12 However, to our knowledge, this is the first study that compares the hemodynamic profiles of the large and small orifices and the potential impact of functional and nonfunctional MR. Specifically, this study is the first to compare the VTi of each orifice. Regardless of the discrepant sizes of large to small orifice, our results show that the VTi of each orifice is equal. This holds irrespective of the mechanism of MR prior to MVCC. Therefore, it is feasible to calculate a total or summed MVA using the continuity equation, provided that MR is reduced to less than moderate severity.
Our data are also of great importance because MVA calculation from VTi could be easily applied to transthoracic echocardiography, as VTi requires Doppler alignment with only 1 orifice. This is particularly important when applying transthoracic echocardiography to derive MVA after MVCC, as 3D imaging may not always be feasible.
Study limitations. The study population was relatively small. However, to our knowledge, this is the first study to show that the hemodynamics between the large and small MV orifices after MVCC are the same irrespective of functional vs nonfunctional MR, and therefore allows calculation of the continuity equation of the total MVA, provided that MR is less than moderate. Further studies comparing VTi-derived vs 3D-determined dual-MV orifice areas would be of great interest.
Conclusion

The MV inflow hemodynamics of large vs small orifices after MVCC are the same irrespective of MR mechanism. This allows for the calculation of total MVA using the continuity equation. Furthermore, this facilitates calculation of MVA during MVCC and should aid in the assessment of procedural success by avoiding clinically significant iatrogenic mitral stenosis. Further studies using 3D imaging to measure large and small MV orifice areas after MVCC to compare with continuity-derived total MVA are of great interest.
Affiliations and Disclosures
From 1the University of Louisville, Division of Cardiovascular Medicine, Louisville, Kentucky; 2Emory University, Department of Surgery, Atlanta, Georgia; and 3the University of Louisville, Department of Anesthesiology, Louisville, Kentucky.
Disclosure: The authors have completed and returned the ICMJE Form for Disclosure of Potential Conflicts of Interest. The authors report no conflicts of interest regarding the content herein.
Manuscript accepted November 29, 2021.
The authors report that patient consent was provided for publication of the images used herein.
Address for correspondence: Marcus F. Stoddard, MD, FASE, 550 South Jackson Street, Ambulatory Care Building, 3rd floor, Cardiovascular Medicine Division, Louisville, KY 40402. Email: mfstod01@louisville.edu
References
1. Baskett RJ, Exner DV, Hirsch GM, Ghali WA. Mitral insufficiency and morbidity and mortality in left ventricular dysfunction. Can J Cardiol. 2007;23(10):797-800. doi:10.1016/s0828-282x(07)70830-9
2. Nkomo VT, Gardin JM, Skelton TN, Gottdiener JS, Scott CG, Enriquez-Sarano M. Burden of valvular heart diseases: a population-based study. The Lancet. 2006;368(9540):1005-1011. doi:10.1016/S0140-6736(06)69208-8
3. Feldman T, Kar S, Elmariah S, et al. Randomized comparison of percutaneous repair and surgery for mitral regurgitation: 5-year results of EVEREST II. J Am Coll Cardiol. 2015;66(25):2844-2854. doi:10.1016/j.jacc.2015.10.018
4. Stone GW, Lindenfeld J, Abraham WT, et al. Transcatheter mitral-valve repair in patients with heart failure. N Engl J Med. 2018;379(24):2307-2318. doi:10.1056/NEJMoa1806640
5. Mack MJ, Abraham WT, Lindenfeld J, et al. Cardiovascular outcomes assessment of the MitraClip in patients with heart failure and secondary mitral regurgitation: design and rationale of the COAPT trial. Am Heart J. 2018;205:1-11. doi:10.1016/j.ahj.2018.07.021
6. Mauri L, Foster E, Glower DD, et al. 4-year results of a randomized controlled trial of percutaneous repair versus surgery for mitral regurgitation. J Am Coll Cardiol. 2013;62(4):317-328. doi:10.1016/j.jacc.2013.04.030
7. Biaggi P, Felix C, Gruner C, et al. Assessment of mitral valve area during percutaneous mitral valve repair using the MitraClip system: comparison of different echocardiographic methods. Circ Cardiovasc Imaging. 2013;6(6):1032-1040. doi:10.1161/CIRCIMAGING.113.000620
8. House CM, Nelson WB, Nickele GA, Ahmed I, Dahiya R. Mitral valve area by the pressure half-time method does not correlate with mean gradient in mitral valve repair patients. Eur J Echocardiogr. 2011;12(2):124-130. doi:10.1093/ejechocard/jeq162
9. Thomas J, Wilkins G, Choong C, et al. Inaccuracy of mitral pressure half-time immediately after percutaneous mitral valvotomy. Dependence on transmitral gradient and left atrial and ventricular compliance. Circulation. 1988;78(4):980-993. doi:10.1161/01.cir.78.4.980
10. Zoghbi WA, Enriquez-Sarano M, Foster E, et al. Recommendations for evaluation of the severity of native valvular regurgitation with two-dimensional and Doppler echocardiography. J Am Soc Echocardiogr. 2003;16(7):777-802. doi:10.1016/S0894-7317(03)00335-3
11. Siegel RJ, Biner S, Rafique AM, et al. The acute hemodynamic effects of MitraClip therapy. J Am Coll Cardiol. 2011;57(16):1658-1665. oi:10.1016/j.jacc.2010.11.043
12. Thaden JJ, Malouf JF, Nkomo VT, et al. Mitral valve anatomic predictors of hemodynamic success with transcatheter mitral valve repair. J Am Heart Assoc. 2018;7(2):e007315. Published 2018 Jan 13. doi:10.1161/JAHA.117.007315